Studiengang: Geometrie und Topologie

Studiengang: Geometrie und Topologie

Copyright (C) 1984 by Thaves.

Nicht-Euklidische Geometrien

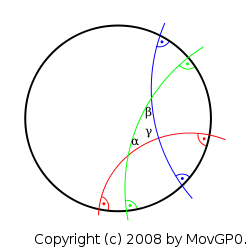Euklids 5. Axiom, das Parallelenaxiom, besagt: "In einer Ebene gibt es zu jeder Geraden G und jedem Punkt P ausserhalb von G genau eine Gerade, die zu G parallel ist und durch den Punkt P geht". Über 2000 Jahre lang versuchten Mathematiker vergeblich, dieses Axiom aus den übrigen Axiomen herzuleiten.  Im 19. Jahrhundert zeigten Gauss, Lobatschewski und Bolyai die Unmöglichkeit einer solchen Herleitung: Sie konstruierten ebene Geometrien, die alle übrigen Axiome der euklidischen Geometrie erfüllen, das Parallelenaxiom jedoch nicht. Ein einfaches Modell einer solchen Geometrie ist die hyperbolische Ebene: In dieser Geometrie ist die "Ebene" durch die Kreisscheibe repräsentiert, "Geraden" sind Kreissegmente senkrecht zum Rand der Kreisscheibe, und Winkel sind wie üblich. Das Bild rechts zeigt, dass die Winkelsume im Dreieck in dieser Geometrie kleiner als 180 Grad ist. Das Parallelenaxiom ist verletzt, denn durch jeden Punkt ausserhalb einer "Geraden" G gibt es unendlich viele "Geraden", die zu G parallel sind (d.h. G nicht schneiden).

Riemannsche Geometrie

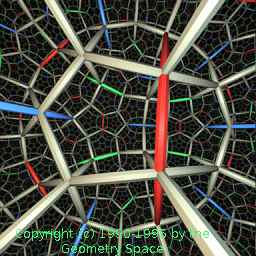In seiner Antrittsvorlesung "Über die Hypothesen, welche der Geometrie zu Grunde liegen" im Jahre 1854 entwickelte Bernhard Riemann die Idee von Geometrien in einer beliebigen Dimension n. Die Definitionen von Geraden, Längen, Winkeln etc verallgemeinern sich auf solche Riemannschen Mannigfaltigkeiten. Ausserdem gibt es ein Konzept von "Krümmung", das die Abweichung einer solchen Riemannschen Geometrie von der Euklidischen misst. Die oben erwähnte hyperbolische Ebene ist negativ gekrümmt, während die Oberfläche einer Kugel positiv gekrümmt ist. Das Bild rechts zeigt den Blick in einen 3-dimensionalen negativ gekrümmten Raum; das Video Not Knot (Sehen Sie hier Teil 1 und hier Teil 2.)  lässt die Zuschauer durch einen solchen Raum fliegen.
Einsteins Entdeckung der Allgemeinen Relativitätstheorie brachte 1915 die Riemannsche Geometrie schlagartig in den Blickpunkt der Öffentlichkeit. In dieser Theorie ist die Raumzeit eine 4-dimensionale (pseudo-)Riemannsche Mannigfaltigkeit, deren Krümmung die die Gravitation widerspiegelt.

Geometrie heute

Felix Kleins Erlanger Programm führte 1872 zu einer gewaltigen Erweiterung des Geometriebegriffes. Klein charakterisiert eine Geometrie als das Studium von Grössen, die unter bestimmten Transformationen invariant bleiben. So sind Längen und Winkel invariant unter Verschiebungen, Drehungen und Spiegelungen, und dies führt zur Riemannschen Geometrie. Eine andere Geometrie ergibt sich zum Beispiel, wenn man sich nur für Volumina interessiert. Diese sind invariant unter Verschiebungen, Drehungen und Spiegelungen, aber auch unter vielen weiteren Transformationen wie Strecken in einer Richtung und Stauchen in einer anderen. In dieser "Volumen-Geometrie" gibt es also mehr zulässige Transformationen, dafür aber keine Messungen von Längen und Winkeln.
Einige wichtige Gebiete der modernen Geometrie sind die folgenden: Die Erweiterung der reellen Zahlen zu den komplexe Zahlen führt zur komplexen Geometrie. In der algebraischen Geometrie untersucht man Fragen der Zahlentheorie wie die 1995 bewiesene Fermat-Vermutung. Die symplektische Geometrie beschäftigt sich mit geometrischen Strukturen in der Physik, von der Himmelsmechanik bis zur String-Theorie.

Topologie

Im Gegensatz zur Geometrie interessiert sich die Topologie nicht für die genaue Form eines Objektes, sondern nur für die Eigenschaften, die unter beliebigen kontinuierlichen Deformationen erhalten bleiben. So sind eine Kaffeetasse und ein Autoreifen ineinander deformierbar und deshalb "topologisch gleich". Eine Kugel ist hingegen von diesen topologisch verschieden: In der Kugel lässt sich jede geschlossene Kurve auf einen Punkt zusammenziehen, in der Kaffeetasse hingegen nicht (wenn die Kurve einmal über den Henkel läuft), und diese Eigenschaft ist invariant unter kontinuierlichen Deformationen. Eine berühmte Vermutung von Poincaré besagt, dass jede kompakte dreidimensionale Mannigfaltigkeit ohne Rand (die verhergehenden Beispiele haben alle einen Rand, z.B. die Kugeloberfläche), in der sich jede geschlossene Kurve auf einen Punkt zusammenziehen lässt, topologisch gleich ist zur Oberfläche der vierdimensionalen Kugel. Diese 1904 aufgestellte Vermutung wurde 2003 von Perelman bewiesen.